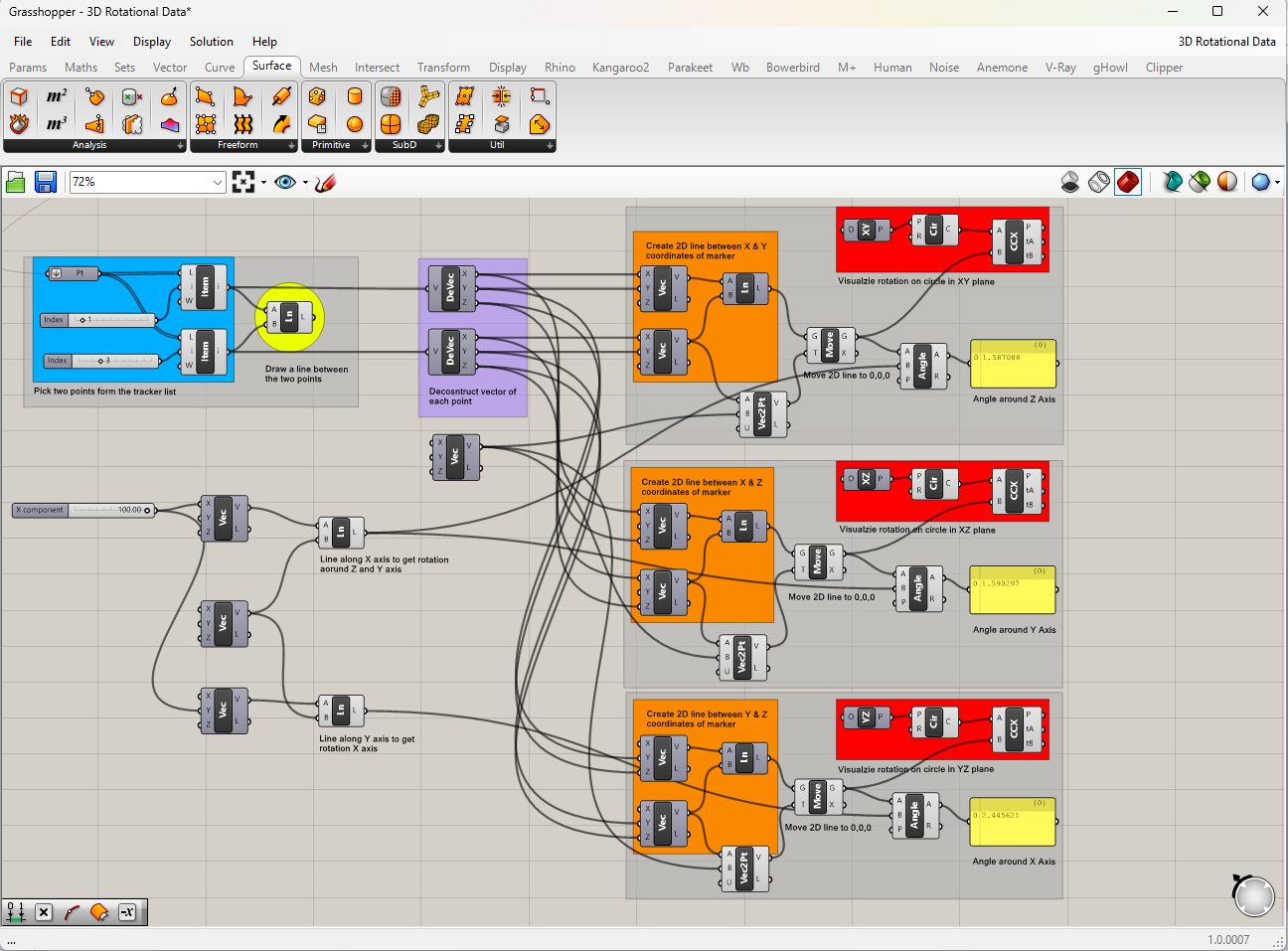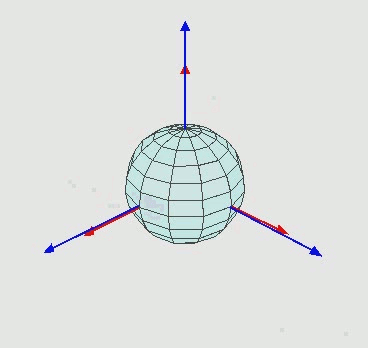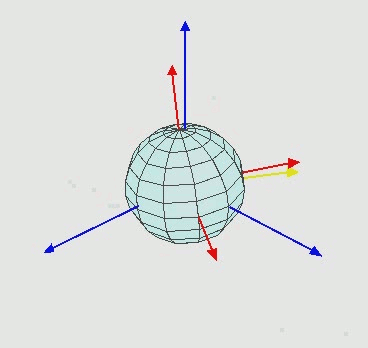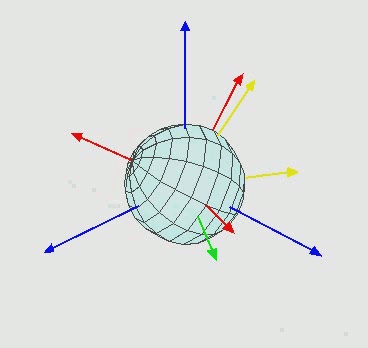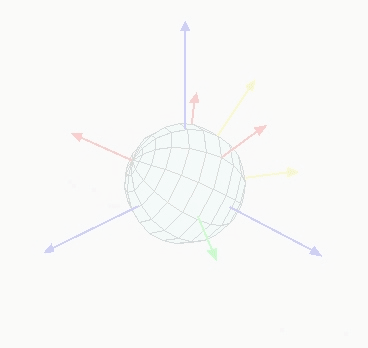

If you were to draw a line between two markers that line would have multi-axis rotation as you move the object. That 3D rotation can be measured through three angles. The most common way to measure these angles is through Euler Angles. Typically the first angle is a rotation around the Z axis and then a rotation around the X axis with the third being a Z rotation around the current axis of rotation or Z-X-Z angles.
In this definition we are deconstruct the vector of each marker and then remaking a 2D line with only two of its coordinates for instance just X and Y or X and Z. This allows to get the angle of rotation between that 2D line and a line along the cardinal planes. You can download the above definition here: 3D Rotational Data